Number System Conversion
In this page we will only focus on building the most easiest mental model for number systems and conversions. Just to ensure that the conversions are registered in mind forever. Mathematically, we use division and multiplication methods for conversions between number systems.
Odometer Mental Model
Look at all number systems with one mental model that's the odometer. In a odometer,
- Each position can start from minimum value of 0 to maximum value of base - 1.
- When we increment the value at a position beyond maximum value, it rolls over to 0 and increments the next position by 1.
- Then again the current position can be incremented from 0 to maximum value.
This is exactly how all number systems work. In case of binary, the allowed values are just 0 and 1. So the numbers are just 0, 1, 10, 11, 100, 101, 110, 111, 1000, etc.
Box model for conversions
See every position in a number system as box size and each position has hold only certain number of boxes which is a fixed value for that based system. For example, in case of base 10, each position can hold 10 boxes of different sizes.
The boxes at higher position are groups of boxes already created at previous position. For example, in base 10, the box at position 2 (hundreds) contains 10 boxes but each box is actually 10 boxes of size 10 (tens).
| Position | Binary (base-2) | Decimal (base-10) | Hexadecimal (base-16) |
|---|---|---|---|
| 0 | 0-1 boxes of size 1 | 0-9 boxes of size 1 | 0-15 boxes of size 1 |
| 1 | 0-1 boxes of size 2 | 0-9 boxes of size 10 | 0-15 boxes of size 16 |
| 2 | 0-1 boxes of size 4 | 0-9 boxes of size 100 | 0-15 boxes of size 256 |
| 3 | 0-1 boxes of size 8 | 0-9 boxes of size 1,000 | 0-15 boxes of size 4,096 |
| 4 | 0-1 boxes of size 16 | 0-9 boxes of size 10,000 | 0-15 boxes of size 65,536 |
| 5 | 0-1 boxes of size 32 | 0-9 boxes of size 100,000 | 0-15 boxes of size 1,048,576 |
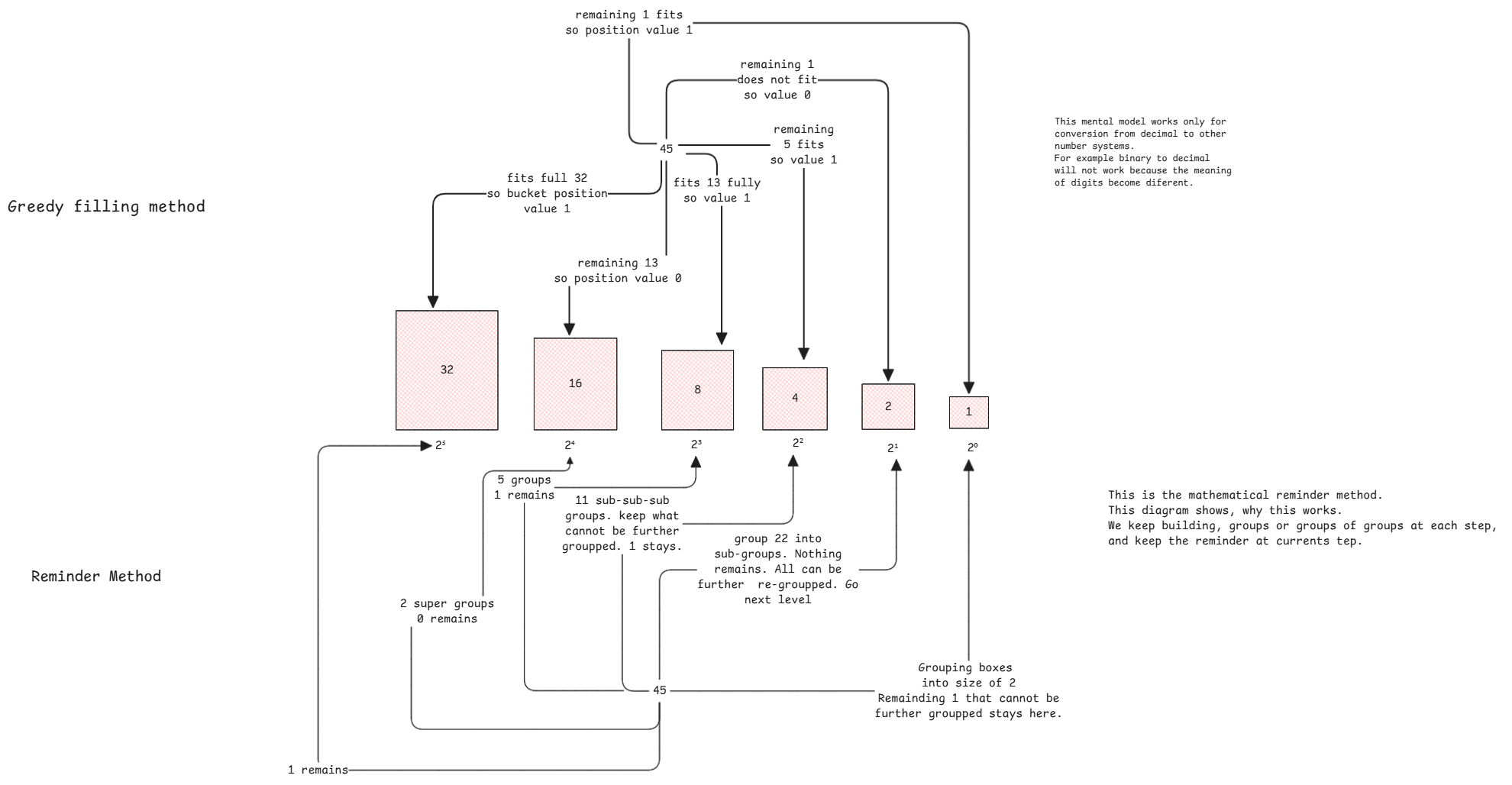
1.Greedy model conversion - Put the maximum possible items in a boxes at each position. The boxes must be always full and move remaining to next position. If no box can be full, then set the position value to 0.
2.Remainder Model - At each position, we divide/group by the items that can fit in that box. For every division, the remainder says what doesn't fit in the next box and goes to the current position. For the next division, we re-group/re-divide the quotient again. This works since the boxes of next position are always multiple of current position boxes. So we just continue building groups of groups (boxes of boxes).
Division is nothing but making groups of certain size.
If we keep dividing again, we only make group of groups. This is exactly how the remainder model relates to the box mental model.
- Non decimal to decimal conversion - We use weighted sum model. Each position's value is multiplied by the box size for that position and all such products are summed to get the decimal value.
Mathematical Conversions
- From Base 10 - Divide by the destination base system and keep remainder for that position.
- To Base 10 - Multiply each position by the base system value for that position (box size) and add them.
Conversion between non-decimal systems is mathematically possible but very hard to do multiplication and division using any other number system.
So we use decimal as an intermediate step always.
Direction of Reading Digits
-
Right to Left - In this method, the full number must read first. Then we know which number is in which position. Since value comes from position which is the box size.
-
Left to Right - This is the intuitive way of reading and also how computers implement conversion. Always assumes that there is just one digit and processes just one position at a time.
- Every position is processed assuming to be the last position.
- Means, every position is just taken value as it's since last position has power of 0.
- Then rest of the position is multiplied by the base value.
Multiplying the already added value by base value is equivalent to shifting the entire number. So we only add the new number to the existing number.