Sine and Cosine

Sine and cosine are periodic trigonometric functions. They relate to the unit circle.

what's Trigonometry

It's a branch of math. It studies the links between the angles and sides of triangles, mostly right triangles.

Trigon in Greek means triangle.

Polar to Cartesian Conversion

The Cartesian way is the most common way to show co-ordinates. It uses the x and y axes. The Polar System uses the radius length and the angle from the x-axis.

Trigonometry gives us a way to convert between these two systems.

$$\begin{aligned} x = r(cos(θ)) \\ y = r(sin(θ)) \end{aligned}$$

multiplicate with radius

All trigonometric functions are multiplied by the radius. The reason is that sine and cosine assume a 'unit circle'. That's a circle with radius 1.

The circumference is 2πR, which is 2π for a unit circle.

This is also why graphs show the x-axis with π or 2π as the time for one full cycle.

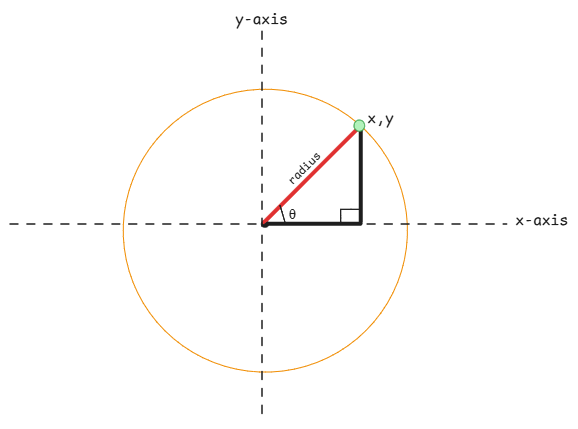
Circle

This is where sine and cosine come from. A point rotates on the circle. Its co-ordinates give the sine and cosine values.

• cosine - x co-ordinate of the point on the circle.
• sine - y co-ordinate of the point on the circle.

Radian in a circle

A radian is the length of an arc on the circle. One radian equals the length of the radius.

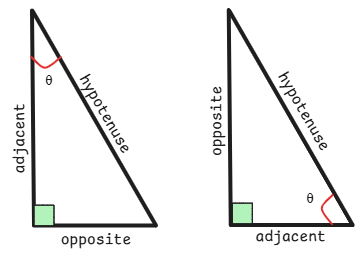
Triangle

You can find sine and cosine from a right triangle. Place the triangle inside a unit circle. Then use the formulas below:

$$\begin{aligned} sine = \frac{\text{opposite}}{\text{hypotenuse}} \\ cosine = \frac{\text{adjacent}}{\text{hypotenuse}} \end{aligned}$$

opposite and adjacent is relative

Opposite and adjacent are relative to the angle θ. This angle depends on which of the two angles you pick.

Oscillations

It's just a coincidence that oscillations fit sine and cosine. These include a swing, a pendulum, and sound waves.

That's why physics uses these functions to describe waves and motion.

No relation to circle or triangle

It has no real link to a circle or triangle here. The motion just forms the same sine shape. We use these functions.

Inputs to Sine and Cosine Functions

Theta

When you evaluate sine and cosine, the angle is the input. It's often written as θ, or "theta." The function doesn't really use this input.

It just shows that x and y relate to the angle θ in the unit circle. As the angle changes, x and y change too. And x and y are the outputs of cosine and sine.

Time

For oscillations, time is often the input. As time moves on, the angle θ changes. That in turn changes the sine and cosine values.

Time Dependency

The x-axis shows the co-ordinates of the moving point. In real life, though, it stands for time.

Frequency

Frequency is how fast the event finishes one full cycle. For an object going around the unit circle, it depends on how fast the angle θ changes with time.

useful links

• visualization[https://setosa.io/ev/sine-and-cosine/]

Sine and Cosine in Computation

Computers have no idea of angles or triangles. They only know numbers. They compute sine and cosine with math formulas.

The libraries that build these functions use the Taylor series to find the values.

GPS Co-ordinates

GPS co-ordinates use latitude and longitude, which are angles. Sine and cosine turn these angles into Cartesian co-ordinates. This gives the position on the Earth's surface.

Without the Cartesian co-ordinates, you can't find the exact distance between two GPS points.

GPS is just angles

• Latitude - the angle from the equator to the point on the Earth's surface. It gives the north-south position.
• Longitude - the angle from the prime meridian to the point on the Earth's surface. It gives the east-west position.