Number Series

It's important to understand how different number series can be interpreted and sum of the series is derived. This is necessary in general and specifically for big O calculations.

Here it's important to keep in mind that the value at each position can be derived from previous positions. This is exactly why the sum in the series is represented just using the last elements in most cases.

It's all about finding the area in geometry

In all the sum series, the objective is to find the area based on the series. The sum in the sequence represents the sum of area created by each position.

meaning of N in the series

Here N doesn't mean the value at the position. N means the position itself. Consider this for all N's in the below table.

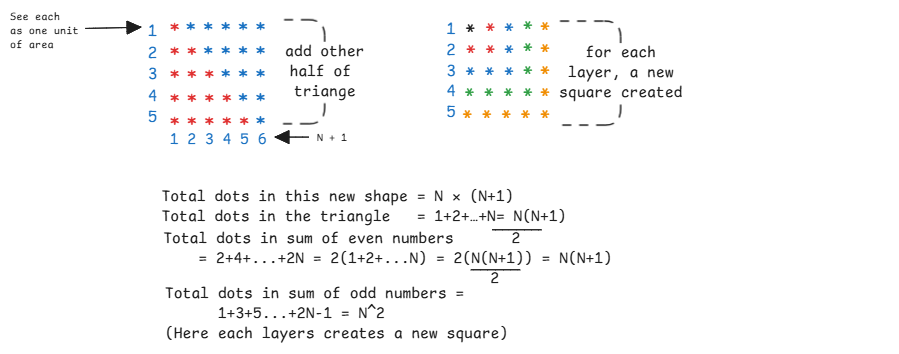
Example in case of sum of odd numbers, the N in $N^2$ refers to the last position of the list.

Number series / pattern	Formula / closed form	Why it appears in interviews
Arithmetic series	$S = N(\frac{first + last}{2})$	Iteratively adding a constant to each position.
Sum of first N numbers	$1 + 2 + ... + N = \frac{N(N+1)}{2}$	Counting loop iterations, triangular loops. Same as above. But adding 1 to each position.
Sum of 1 through N−1	$1 + 2 + 3 + ... + (N−1) = \frac{N(N−1)}{2}$	Pair comparisons, nested loops. Same rectangle mental model. Just one layer less.
Sum of odd numbers	$1 + 3 + ... + (2N−1) = {N^2}$	Explains quadratic growth. Here 2N-1 is the value at each position. Eg., 2x1-1, 2x2-1.
Sum of even numbers	$2 + 4 + 8 + ... + 2N = N(N+1)$	Loops skipping by 2. Here 2N is the value at each position. Eg., 2x1, 2x2.
Sum of powers of two	$1 + 2 + 4 + ... + 2ⁿ = {2^{n+1}−1}$	Trees, recursion trees, BFS/DFS
Geometric series	$1 + r + r² + ... + rⁿ = \frac{r^{n+1}−1}{r−1}$	Divide-and-conquer analysis
Harmonic series	$1 + 1/2 + 1/3 + ... + 1/N ≈ log N$	Amortized analysis (hashing, resizing)
Average of 1 to N	$\frac{N + 1}{2}$ ≈ $\frac{N}{2}$	Expected value, amortized cost. Here we take sum of first value and the last value and take its average.
Powers of two	$2^0, 2^1, 2^2, … , 2^n$	Binary structures, divide-and-conquer
Number of pairs	$_n C_2 = \frac{N(N−1)}{2}$	Comparing all pairs. This is just the regular combinations formula.
Number of subsets	$2^n$	Power set, bitmask problems
Number of permutations	$N!$	Backtracking, ordering problems

geometric versus arithmetic series

In geometric series, the elements in the series are multiplied by a constant such that the shape/proportions are preserved.

Whereas in arithmetic series, a constant is only added to each element of the series.

Meaning of terms

• power set - Explained here.
• Harmonic series - The name is related to music instruments and how different string length generate different sounds.
• Bit mask - Explained here.
• Number of pairs - This is also used for same use cases where there are nested for loops. Similar to Sum of 1 through N−1.

Mental models for remembering formulae

Since the above formulas list is a long one, its necessary to have mental models that remains in memory forever.

Geometry is the origin of everything

Using geometry as the mental model will help us to remember the number series formulae.

Arithmetic Series

Geometric Series

Here each position in the series is proportional to the previous one. Since the base of the exponent is the variable here, the geometric size at each step depends both base and exponent.

$$\begin{aligned} r = \frac{\text{next term}}{\text{current term}} \\ \text{Value at next position can be expressed in two ways:} \\ next = r×current \\ next = current+(r−1)×current \\ \text{this is where the extra (r-1) in the sum formula comes from.} x &= \frac{6}{9} = \frac{2}{3} \end{aligned}$$

mental model for geometric series

It looks a bit confusing since we use mostly the $r^{n+1}$ to get the sum of all numbers until $r^n$. This is because each term is multiplied by $r$ which makes the next term way bigger than previous one.

Another analogy is, every next term already contains all the parts of the previous series.