Knuth-Morris-Pratt Algorithm

This algorithm is one of the many algorithms used for pattern searching.

Brut force algorithm

Naive pattern matching runs at $0(M*N)$. It's the sliding window method by moving the pattern one bit at a time on the entire string.

It doesn't understand what the pattern contains. This is exactly what the KMP algorithm solves.

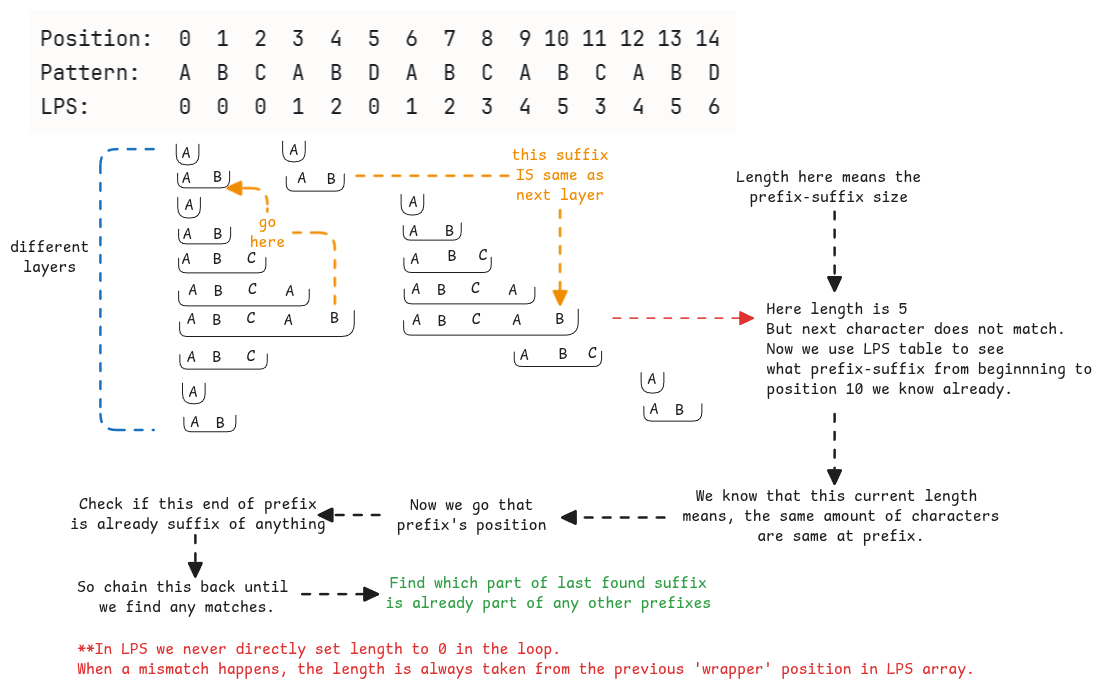
LPS - Longest Prefix Suffix

This is the foundation of KMP. We must build the LPS array of the entire pattern string beforehand to use LPS.

LPS and KMP looks similar

While creating the LPS array of the pattern string, it looks similar to KMP since even here we don't go through the entire string to find prefixes and suffixes.

Mental Model

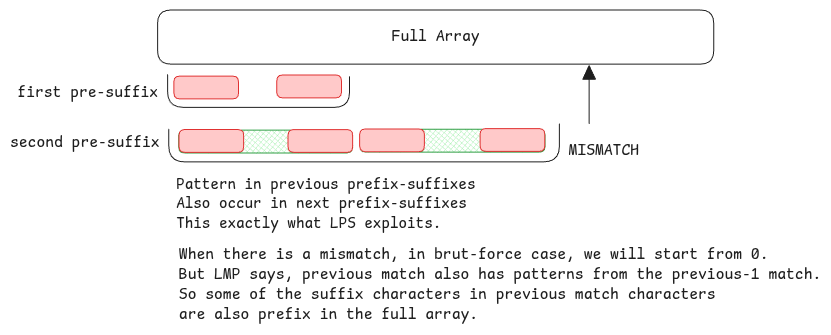
When a mismatch happens

• we go the prefix of the previous match.
• Check if any character after previous prefixes matches the mismatch.

why $length - 1$ is mentioned everywhere

length variable in all the explanations means the length of the last found longest prefix-suffix.

But length starts it's count from 1 where as the LPS array index from 0. Hence, when the LPS array is queried, we always do an $lps[length - 1]$.

How KMP uses LPS?

As all pattern matches, we've two pointers. One for the actual string and the one for the pattern. We move both whenever there are matches. But when there is a mismatch, we move only the pointer of the pattern string back. How much we must move back is what the LPS index provides.

The approach of moving the pointer back is actually bit counter intuitive. We're not moving anything back. In fact, we're sliding the matching window forward because we know that characters equal to longest prefix suffix until the previous match will anyways still match.

why does LPS help with KMP pattern search?

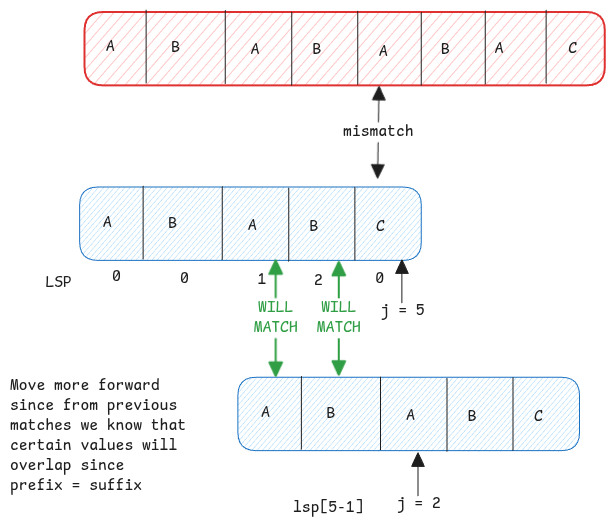
The LMP array tells us that the last $lps[len - 1]$ characters you matched are the same as the first $lps[len - 1]$ characters.

This base logic is important to be remembered.